Understanding the determinant of a 2x2 matrix is a fundamental concept in linear algebra, crucial for solving systems of equations, finding the inverse of a matrix, and determining the properties of a matrix. The determinant of a 2x2 matrix can be calculated using a simple formula, which provides insights into the matrix's behavior and its applications in various fields such as physics, engineering, and computer science.
Introduction to 2x2 Matrices and Determinants

A 2x2 matrix is a square matrix with two rows and two columns, typically represented as:
| a | b |
|---|---|
| c | d |
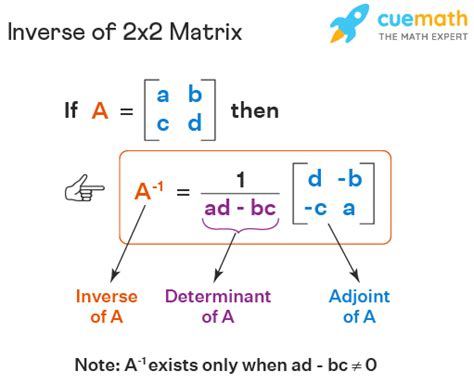
where a, b, c, and d are the elements of the matrix. The determinant of this matrix, denoted as det(A) or |A|, can be calculated using the formula: det(A) = ad - bc. This formula is derived from the method of expansion by minors along any row or column.
Calculating the Determinant of a 2x2 Matrix
The calculation of the determinant is straightforward and involves simple arithmetic operations. For example, given a matrix:
| 2 | 3 |
|---|---|
| 4 | 5 |
the determinant would be (2*5) - (3*4) = 10 - 12 = -2. This determinant value provides information about the matrix’s invertibility and its geometric interpretation, such as the scaling effect on areas when the matrix is used as a transformation.
Key Points
- The determinant of a 2x2 matrix A, with elements a, b, c, and d, is calculated as ad - bc.
- A non-zero determinant indicates that the matrix is invertible, which is crucial for solving systems of linear equations and understanding the matrix's transformation properties.
- The determinant can be positive or negative, with the sign indicating the orientation of the transformation in the plane.
- A determinant of zero indicates that the matrix is singular, meaning it does not have an inverse and may not be able to represent all possible transformations.
- Understanding determinants is fundamental for various applications in science, engineering, and computer graphics, where matrices are used to represent transformations, solve systems of equations, and analyze the properties of linear systems.
Applications and Interpretations of the Determinant
The determinant of a 2x2 matrix has several applications and interpretations. In geometry, it represents the area scaling factor of the transformation described by the matrix. In physics and engineering, matrices and their determinants are used to describe complex systems, solve problems involving systems of linear equations, and analyze the properties of materials and structures.
Geometric Interpretation
Geometrically, the determinant of a 2x2 matrix represents how the area of a figure changes when the matrix is applied as a linear transformation. A positive determinant indicates that the transformation preserves the orientation of the figure, while a negative determinant indicates a reflection. The absolute value of the determinant gives the factor by which the area is scaled.
For instance, a determinant of 2 means that the area of any figure transformed by the matrix will be twice the original area, while a determinant of -1/2 means the area will be halved and the figure will be reflected.
| Determinant Value | Geometric Effect |
|---|---|
| Positive | Orientation preserved, area scaled by |det| |
| Negative | Orientation reversed, area scaled by |det| |
| Zero | Singular transformation, area reduced to zero |
What does a determinant of zero mean for a 2x2 matrix?
+A determinant of zero indicates that the matrix is singular, meaning it does not have an inverse. This implies that the transformation represented by the matrix will reduce any area to a line or a point, effectively collapsing the space.
How does the determinant affect the invertibility of a matrix?
+A non-zero determinant is a necessary and sufficient condition for a 2x2 matrix to be invertible. If the determinant is zero, the matrix does not have an inverse, meaning it cannot be used to solve systems of linear equations uniquely.
What is the practical significance of the determinant in real-world applications?
+In practical terms, the determinant is crucial for solving systems of linear equations, which are ubiquitous in physics, engineering, economics, and computer science. It also plays a role in computer graphics, where matrices are used to perform transformations on images and objects.
In conclusion, the determinant of a 2x2 matrix is a fundamental concept in linear algebra, providing crucial information about the matrix’s properties and its applications in various fields. Understanding how to calculate and interpret the determinant is essential for working with matrices and applying linear algebra principles in real-world problems.
