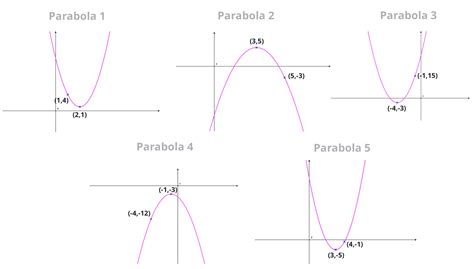
Graphing parabolas is a fundamental concept in algebra and geometry, allowing us to visualize and analyze the behavior of quadratic equations. A parabola is defined as the set of all points that are equidistant to the focus and the directrix, and its graph can be represented by a U-shaped curve. To graph a parabola, we need to understand the key components that define its shape and position, including the vertex, axis of symmetry, and the direction of opening.
Key Points
- The standard form of a quadratic equation is $ax^2 + bx + c$, where $a$, $b$, and $c$ are constants.
- The vertex form of a quadratic equation is $a(x - h)^2 + k$, where $(h, k)$ is the vertex of the parabola.
- The axis of symmetry is a vertical line that passes through the vertex, given by the equation $x = h$.
- The direction of opening is determined by the sign of $a$, with $a > 0$ indicating a parabola that opens upwards and $a < 0$ indicating a parabola that opens downwards.
- The focus and directrix of a parabola can be used to determine its shape and position.
Understanding the Standard Form of a Quadratic Equation
The standard form of a quadratic equation is ax^2 + bx + c, where a, b, and c are constants. To graph a parabola, we need to identify the values of a, b, and c and use them to determine the vertex, axis of symmetry, and direction of opening. The value of a determines the direction of opening, with a > 0 indicating a parabola that opens upwards and a < 0 indicating a parabola that opens downwards.
Converting to Vertex Form
To graph a parabola, it is often helpful to convert the quadratic equation to vertex form, a(x - h)^2 + k, where (h, k) is the vertex of the parabola. The vertex form allows us to easily identify the vertex and axis of symmetry, making it easier to graph the parabola. The vertex form can be obtained by completing the square, which involves manipulating the quadratic equation to express it in terms of a perfect square trinomial.
| Quadratic Equation | Vertex Form |
|---|---|
| $x^2 + 6x + 8$ | $(x + 3)^2 - 1$ |
| $x^2 - 4x - 3$ | $(x - 2)^2 - 7$ |
Graphing the Parabola

Once we have the vertex form of the quadratic equation, we can graph the parabola by plotting the vertex and using the axis of symmetry to determine the shape of the curve. The axis of symmetry is a vertical line that passes through the vertex, given by the equation x = h. The direction of opening is determined by the sign of a, with a > 0 indicating a parabola that opens upwards and a < 0 indicating a parabola that opens downwards.
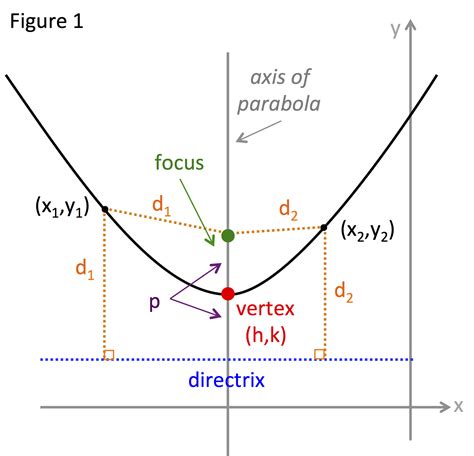
Using the Focus and Directrix
The focus and directrix of a parabola can be used to determine its shape and position. The focus is a point located on the axis of symmetry, and the directrix is a line perpendicular to the axis of symmetry. The parabola is defined as the set of all points that are equidistant to the focus and the directrix. By using the focus and directrix, we can determine the shape and position of the parabola and graph it accurately.
| Focus | Directrix |
|---|---|
| (0, 1) | y = -1 |
| (2, 0) | x = -2 |
Real-World Applications
Graphing parabolas has numerous real-world applications, including physics, engineering, and economics. Parabolas are used to model the trajectory of projectiles, the shape of satellite dishes, and the behavior of economic systems. By understanding how to graph parabolas, we can analyze and predict the behavior of these systems, making it a crucial skill in a variety of fields.
What is the standard form of a quadratic equation?
+The standard form of a quadratic equation is $ax^2 + bx + c$, where $a$, $b$, and $c$ are constants.
How do I convert a quadratic equation to vertex form?
+To convert a quadratic equation to vertex form, complete the square by manipulating the equation to express it in terms of a perfect square trinomial.
What is the axis of symmetry of a parabola?
+The axis of symmetry is a vertical line that passes through the vertex, given by the equation $x = h$.
Graphing parabolas is a fundamental concept in algebra and geometry, with numerous real-world applications. By understanding the key components that define the shape and position of a parabola, including the vertex, axis of symmetry, and direction of opening, we can accurately graph the parabola and analyze its behavior. Whether you are a student, teacher, or professional, mastering the skill of graphing parabolas is essential for success in a variety of fields.