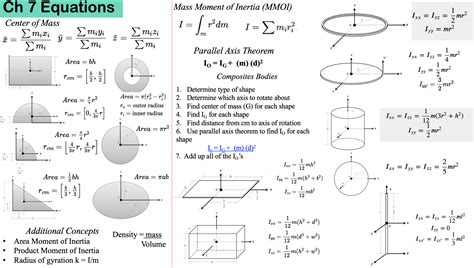
The concept of inertia is a fundamental principle in physics, describing the tendency of an object to resist changes in its state of motion. In the context of complex shapes, understanding inertia is crucial for calculating various physical properties, such as the moment of inertia, which plays a significant role in rotational kinematics and dynamics. The inertia formula, also known as the moment of inertia formula, varies depending on the shape and axis of rotation. This comprehensive guide aims to provide an in-depth exploration of the inertia formula for complex shapes, covering the theoretical foundations, mathematical derivations, and practical applications.
Key Points
- The moment of inertia is a measure of an object's resistance to changes in its rotational motion.
- The inertia formula depends on the shape and axis of rotation, with different formulas for various geometric shapes.
- Calculating the moment of inertia involves integrating the elemental mass moments of the shape with respect to the axis of rotation.
- Complex shapes can be analyzed by decomposing them into simpler shapes and applying the principle of superposition.
- Understanding the inertia formula is essential for designing and optimizing systems involving rotational motion, such as engines, gearboxes, and robotics.
Introduction to Moment of Inertia
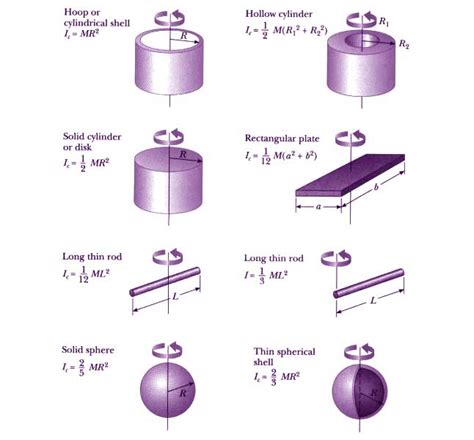
The moment of inertia, denoted by the symbol I, is a measure of an object’s resistance to changes in its rotational motion. It depends on the mass distribution of the object and the axis of rotation. For a point mass, the moment of inertia is simply the product of the mass and the square of the distance from the axis of rotation. However, for complex shapes, the calculation of the moment of inertia requires a more sophisticated approach, involving the integration of elemental mass moments over the entire shape.
Moment of Inertia for Common Shapes
For simple geometric shapes, such as spheres, cylinders, and disks, the moment of inertia can be calculated using well-established formulas. These formulas are derived by integrating the elemental mass moments of the shape with respect to the axis of rotation. For example, the moment of inertia of a sphere rotating about its central axis is given by the formula I = (2⁄5) * m * r^2, where m is the mass of the sphere and r is its radius.
| Shape | Moment of Inertia Formula |
|---|---|
| Sphere | I = (2/5) \* m \* r^2 |
| Cylinder | I = (1/2) \* m \* r^2 |
| Disk | I = (1/2) \* m \* r^2 |
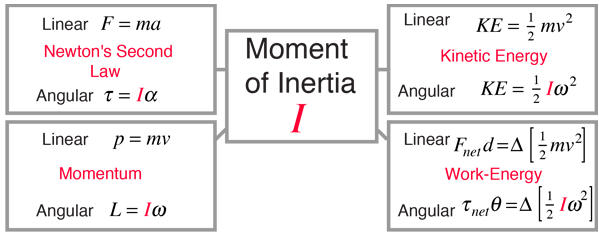
Calculating Moment of Inertia for Complex Shapes
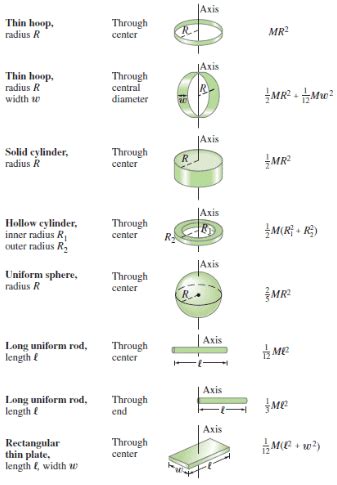
For complex shapes, the calculation of the moment of inertia requires a more nuanced approach. One method involves decomposing the complex shape into simpler shapes, such as spheres, cylinders, and disks, and applying the principle of superposition. This involves calculating the moment of inertia for each individual shape and then combining the results to obtain the total moment of inertia for the complex shape.
Parallel Axis Theorem
The parallel axis theorem is a useful tool for calculating the moment of inertia for complex shapes. It states that the moment of inertia of a shape about a parallel axis is equal to the moment of inertia about the central axis plus the product of the mass and the square of the distance between the two axes. This theorem allows for the calculation of the moment of inertia for complex shapes by combining the moments of inertia of simpler shapes.
Practical Applications of Moment of Inertia
Understanding the moment of inertia is essential for designing and optimizing systems involving rotational motion. In engineering, the moment of inertia plays a critical role in the design of engines, gearboxes, and robotics. For example, the moment of inertia of a rotor in a turbine engine affects its stability and efficiency. In sports, the moment of inertia of a golf club or a tennis racket influences its swing dynamics and performance.
Design Considerations
When designing systems involving rotational motion, engineers must carefully consider the moment of inertia of the components. A higher moment of inertia can provide greater stability and resistance to changes in rotational motion, but it can also increase the energy required to accelerate or decelerate the system. By optimizing the moment of inertia, engineers can improve the performance and efficiency of the system.
What is the moment of inertia, and why is it important?
+The moment of inertia is a measure of an object's resistance to changes in its rotational motion. It is essential for designing and optimizing systems involving rotational motion, as it affects the stability, efficiency, and performance of the system.
How do I calculate the moment of inertia for a complex shape?
+To calculate the moment of inertia for a complex shape, you can decompose the shape into simpler shapes, such as spheres, cylinders, and disks, and apply the principle of superposition. You can also use the parallel axis theorem to simplify the calculation.
What are some practical applications of the moment of inertia?
+The moment of inertia has numerous practical applications in engineering, sports, and other fields. It is essential for designing and optimizing systems involving rotational motion, such as engines, gearboxes, and robotics. It also influences the swing dynamics and performance of golf clubs and tennis rackets.
In conclusion, the inertia formula is a fundamental concept in physics that plays a crucial role in understanding the behavior of complex shapes in rotational motion. By mastering the inertia formula and its applications, engineers and physicists can design and optimize systems involving rotational motion, from robotic arms to aircraft wings. Whether you are a student, a researcher, or a practitioner, this comprehensive guide has provided you with a deep understanding of the inertia formula and its significance in the world of physics and engineering.