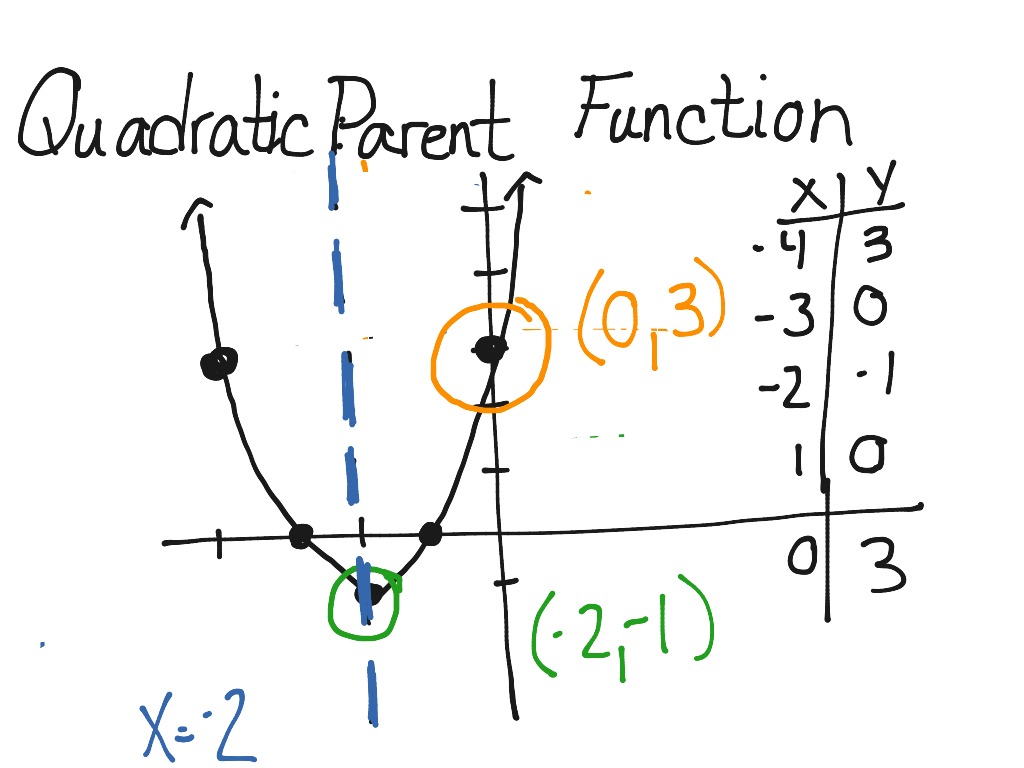
The quadratic parent function, denoted as $f(x) = x^2$, is a fundamental concept in algebra and mathematics. It serves as the foundation for more complex quadratic functions, which are crucial in various fields such as physics, engineering, and economics. Understanding the properties and behavior of the quadratic parent function is essential for analyzing and solving quadratic equations, as well as modeling real-world phenomena.
The graph of the quadratic parent function is a parabola that opens upwards, with its vertex at the origin (0, 0). The parabola is symmetric about the y-axis, meaning that for every point (x, y) on the graph, the point (-x, y) is also on the graph. This symmetry is a characteristic property of even functions, which includes the quadratic parent function. The quadratic parent function has a minimum value of 0 at x = 0, and as x increases or decreases, the function value increases without bound.
Key Points
- The quadratic parent function is $f(x) = x^2$.
- The graph of the quadratic parent function is a parabola that opens upwards with its vertex at (0, 0).
- The parabola is symmetric about the y-axis.
- The quadratic parent function has a minimum value of 0 at x = 0.
- As x increases or decreases, the function value increases without bound.
Properties of the Quadratic Parent Function
The quadratic parent function exhibits several important properties that are essential for understanding its behavior and applications. Some of these properties include:
Domain and Range
The domain of the quadratic parent function is all real numbers, denoted as (-\infty, \infty). This means that the function is defined for every real value of x. The range of the function is all non-negative real numbers, denoted as [0, \infty). This indicates that the function value is always greater than or equal to 0.
Vertex Form
The quadratic parent function can be expressed in vertex form as f(x) = a(x - h)^2 + k, where (h, k) is the vertex of the parabola. For the quadratic parent function, a = 1, h = 0, and k = 0, resulting in the equation f(x) = x^2.
Axis of Symmetry
The axis of symmetry of the quadratic parent function is the vertical line x = 0, which is the y-axis. This line divides the parabola into two congruent halves, reflecting the symmetry of the function.
| Property | Description |
|---|---|
| Domain | All real numbers, $(-\infty, \infty)$ |
| Range | All non-negative real numbers, $[0, \infty)$ |
| Vertex | (0, 0) |
| Axis of Symmetry | x = 0 (y-axis) |
Applications of the Quadratic Parent Function

The quadratic parent function has numerous applications in various fields, including physics, engineering, economics, and computer science. Some examples of these applications include:
Projectile Motion
In physics, the quadratic parent function is used to model the trajectory of projectiles, such as balls, arrows, or rockets. The function describes the relationship between the height of the projectile and its horizontal distance from the launch point.
Optimization Problems
In economics and computer science, quadratic functions are used to model optimization problems, such as maximizing profit or minimizing cost. The quadratic parent function provides a foundation for analyzing and solving these problems.
Geometry and Design
In geometry and design, quadratic functions are used to create curves and shapes, such as parabolas, ellipses, and hyperbolas. The quadratic parent function is a fundamental building block for these geometric forms.
In conclusion, the quadratic parent function is a fundamental concept in mathematics, with far-reaching applications in various fields. Understanding its properties, behavior, and applications is essential for analyzing and solving problems in algebra, geometry, physics, engineering, economics, and computer science.
What is the domain of the quadratic parent function?
+The domain of the quadratic parent function is all real numbers, denoted as (-\infty, \infty).
What is the range of the quadratic parent function?
+The range of the quadratic parent function is all non-negative real numbers, denoted as [0, \infty).
What is the axis of symmetry of the quadratic parent function?
+The axis of symmetry of the quadratic parent function is the vertical line x = 0, which is the y-axis.