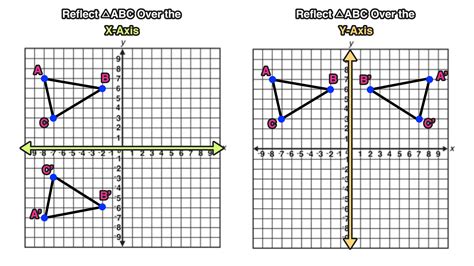
When discussing mathematical transformations, particularly in the context of graphing and coordinate geometry, one fundamental concept is the reflection of a function or a point over the y-axis. This operation involves changing the sign of the x-coordinate of each point on the graph, effectively flipping the graph around the vertical axis. The y-axis, denoted as the line x = 0, serves as the mirror line for this reflection. Understanding how reflections over the y-axis work is crucial for analyzing and manipulating functions, especially in pre-calculus and calculus.
Mathematical Representation

To reflect a point (x, y) over the y-axis mathematically, one simply changes the sign of the x-coordinate, resulting in the new point (-x, y). This transformation applies to all points on a graph, including those representing functions. For a function f(x), its reflection over the y-axis is denoted as f(-x), where each x value in the original function is replaced by -x. This concept is pivotal in understanding symmetry in mathematics, as a function that remains unchanged after a reflection over the y-axis is said to be even.
Graphical Interpretation
Graphically, reflecting a function over the y-axis will flip its graph. For instance, the graph of y = x^2, a parabola that opens upwards, remains unchanged under a reflection over the y-axis because it is symmetric with respect to the y-axis. On the other hand, the graph of y = x^3, which has a point of inflection at the origin and opens upwards to the right and downwards to the left, will appear to be flipped when reflected over the y-axis, resulting in the graph of y = (-x)^3 = -x^3, which opens downwards to the right and upwards to the left.
| Original Function | Reflected Function |
|---|---|
| y = x^2 | y = (-x)^2 = x^2 |
| y = x^3 | y = (-x)^3 = -x^3 |

Applications and Implications
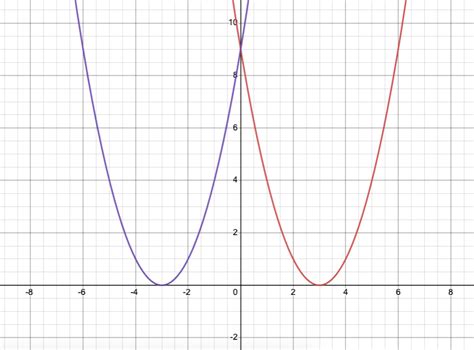
The concept of reflection over the y-axis has far-reaching implications in mathematics and science. In physics, for example, the symmetry of a system can predict its behavior under certain transformations, including reflections. In engineering, understanding how graphs behave under reflections is crucial for designing systems that require symmetry or specific response patterns to inputs. Additionally, in data analysis, recognizing patterns that are symmetric about the y-axis can help in identifying trends and relationships in datasets.
Real-World Examples
In architecture, buildings that are designed to be symmetrical about a central axis (often aligned with the y-axis in a 2D representation) can benefit from this understanding, as it impacts both aesthetics and structural integrity. Similarly, in computer graphics, reflections over axes are fundamental operations used to create realistic environments and manipulate 3D models. The application of reflection principles can also be seen in the design of electronic circuits, where symmetry can affect signal processing and circuit behavior.
Key Points
- Reflection over the y-axis involves changing the sign of the x-coordinate of each point.
- The mathematical representation of a function's reflection over the y-axis is given by f(-x).
- Functions can exhibit symmetry about the y-axis (even functions) or rotational symmetry about the origin (odd functions).
- Understanding reflections is crucial in mathematics, physics, engineering, and data analysis.
- Real-world applications include architecture, computer graphics, and electronic circuit design.
As explored, the concept of reflection over the y-axis is a foundational element in mathematics and its applications, providing insights into symmetry, function behavior, and practical problem-solving across various disciplines. By grasping this concept, individuals can better analyze and understand complex systems, patterns, and designs, ultimately contributing to advancements in science, technology, engineering, and mathematics (STEM) fields.
What is the effect of reflecting a function over the y-axis on its equation?
+Reflecting a function over the y-axis changes the sign of the x variable in its equation, resulting in f(-x) for the original function f(x).
How does the reflection of a point over the y-axis affect its coordinates?
+The reflection of a point (x, y) over the y-axis results in the new point (-x, y), where only the x-coordinate’s sign is changed.
What types of functions remain unchanged after a reflection over the y-axis?
+Even functions, which satisfy the condition f(-x) = f(x) for all x in their domain, remain unchanged after a reflection over the y-axis.