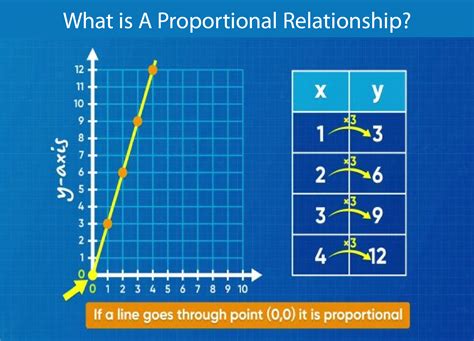
A proportional relationship is a fundamental concept in mathematics that describes a connection between two quantities where one quantity is a constant multiple of the other. This relationship is often represented by the equation y = kx, where y is the dependent variable, x is the independent variable, and k is the constant of proportionality. The constant of proportionality, k, represents the ratio of the change in the dependent variable to the change in the independent variable. In other words, for every unit change in x, there is a corresponding k-unit change in y.
Proportional relationships are characterized by several key features, including a constant rate of change, a straight-line graph, and the ability to be represented by a linear equation. These relationships are commonly observed in various real-world phenomena, such as the relationship between the distance traveled and the time taken, the relationship between the force applied and the resulting acceleration, and the relationship between the cost of an item and its quantity.
Key Points
- A proportional relationship is a connection between two quantities where one quantity is a constant multiple of the other.
- The equation y = kx represents a proportional relationship, where y is the dependent variable, x is the independent variable, and k is the constant of proportionality.
- Proportional relationships are characterized by a constant rate of change, a straight-line graph, and the ability to be represented by a linear equation.
- These relationships are commonly observed in various real-world phenomena, such as distance and time, force and acceleration, and cost and quantity.
- Understanding proportional relationships is essential in various fields, including physics, engineering, economics, and data analysis.
Characteristics of Proportional Relationships
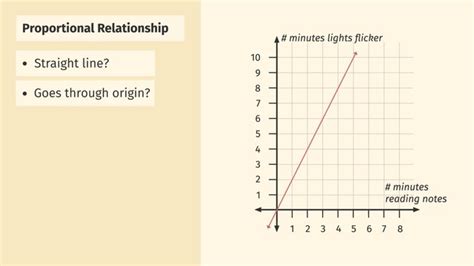
Proportional relationships have several distinct characteristics that set them apart from other types of relationships. One of the primary characteristics is the constant rate of change, which means that the ratio of the change in the dependent variable to the change in the independent variable remains constant. This constant rate of change is represented by the slope of the line in a graph, which is equivalent to the constant of proportionality, k.
Another key characteristic of proportional relationships is the straight-line graph. When a proportional relationship is plotted on a graph, the resulting line is straight, indicating a constant rate of change. This straight-line graph is a visual representation of the linear equation y = kx, which represents the proportional relationship.
Examples of Proportional Relationships
Proportional relationships are abundant in various real-world phenomena. For instance, the distance traveled by a car is directly proportional to the time taken, assuming a constant speed. The force applied to an object is proportional to the resulting acceleration, as described by Newton’s second law of motion. The cost of an item is proportional to its quantity, assuming a constant price per unit.
| Example | Proportional Relationship |
|---|---|
| Distance and Time | Distance = Speed x Time |
| Force and Acceleration | Force = Mass x Acceleration |
| Cost and Quantity | Cost = Price per Unit x Quantity |

Applications of Proportional Relationships
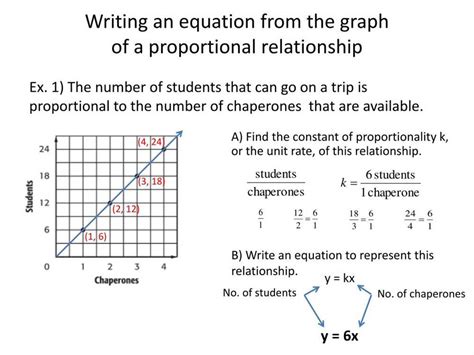
Understanding proportional relationships is essential in various fields, including physics, engineering, economics, and data analysis. In physics, proportional relationships are used to describe the motion of objects, the behavior of forces, and the properties of materials. In engineering, proportional relationships are used to design and optimize systems, such as mechanical systems, electrical circuits, and control systems.
In economics, proportional relationships are used to model the behavior of markets, the impact of policy changes, and the effects of external shocks. In data analysis, proportional relationships are used to identify patterns and trends in data, to make predictions, and to inform decision-making.
Mathematical Representations
Proportional relationships can be represented mathematically using various equations and formulas. The most common representation is the linear equation y = kx, where y is the dependent variable, x is the independent variable, and k is the constant of proportionality. Other representations include the slope-intercept form y = mx + b, where m is the slope and b is the y-intercept, and the point-slope form y - y1 = m(x - x1), where (x1, y1) is a point on the line.
These mathematical representations provide a powerful tool for analyzing and modeling proportional relationships, allowing us to make predictions, identify patterns, and optimize systems.
What is the constant of proportionality in a proportional relationship?
+The constant of proportionality, k, represents the ratio of the change in the dependent variable to the change in the independent variable. It is a constant value that describes the strength of the relationship between the two variables.
How can I identify a proportional relationship in a set of data?
+To identify a proportional relationship, look for a constant rate of change between the variables. You can also plot the data on a graph and check if the resulting line is straight. If the line is straight, it indicates a proportional relationship.
What are some real-world examples of proportional relationships?
+Proportional relationships can be observed in various real-world phenomena, such as the distance traveled by a car and the time taken, the force applied to an object and the resulting acceleration, and the cost of an item and its quantity.
In conclusion, proportional relationships are a fundamental concept in mathematics that describes a connection between two quantities where one quantity is a constant multiple of the other. These relationships are characterized by a constant rate of change, a straight-line graph, and the ability to be represented by a linear equation. Understanding proportional relationships is essential in various fields, including physics, engineering, economics, and data analysis, and has numerous applications in real-world phenomena.